3.1. Timbre of Stringed Instruments

What physical properties of musical instruments give them their specific timbre? In this section, we'll explore the physical properties of strings, or chordophones. These instruments are divided into three major categories (based on the way they receive energy): bowed (like a cello), struck (piano), and plucked (guitar). However, all these instruments share the same mode of vibration - they take the form of a standing wave with nodes on both extremities of the string. So, before we go into stringed instruments, we'll describe a standing wave.

3.1.1. Standing Waves

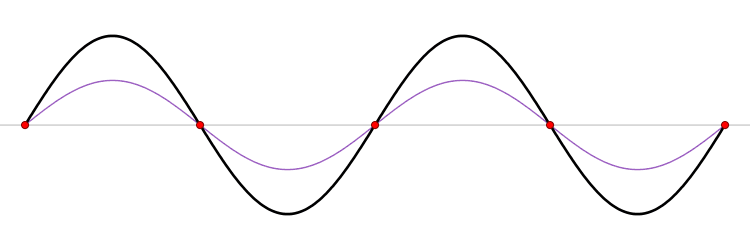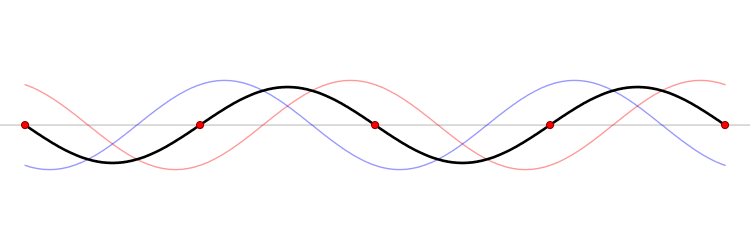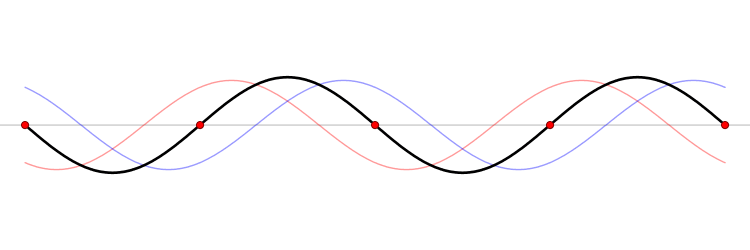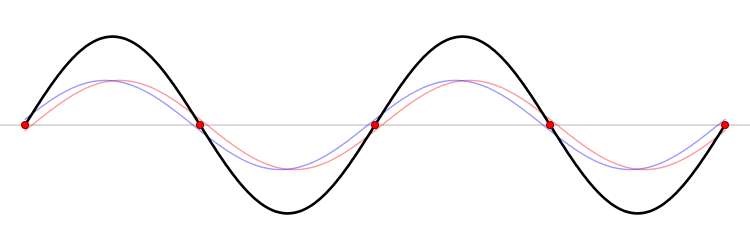
In the image below (from Wikimedia commons), we observe two waves traveling in opposite directions (the blue and red waves). The black wave is the sum of these two waves. Notice how the black wave is stationary - it doesn't travel right or left. The black wave is called a standing wave, because it stands still. Notice the five red dots on the wave. These are called nodes, and they are defined as points on a standing wave which do not change at all. In between each of these nodes is an unmarked antinode, which is defined as a point on a standing wave which changes the most.

Now, not all standing waves are formed by two waves traveling opposite directions, as is shown in this image. For example, a plucked guitar string has to vibrate as a standing wave, because there are nodes at either end of the guitar string. These nodes occur because the string is attached to the guitar body itself at the nut and the bridge, and that attachment cannot vibrate.

In fact, all stringed instruments share this feature - they produce sound through a string that vibrates in a standing wave with nodes at both ends. Additional nodes can form in the middle of the string (like in the animation above), but all stringed instruments MUST have nodes at either end of the string - otherwise they cannot produce sound.

3.1.2. The Physical Nature of Overtones

So how do overtones occur in a string? Our first thought about how a string should vibrate corresponds with the top left string in this animation (from Wikimedia commons):

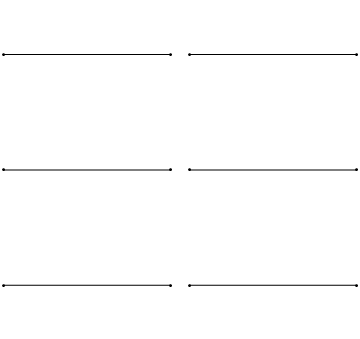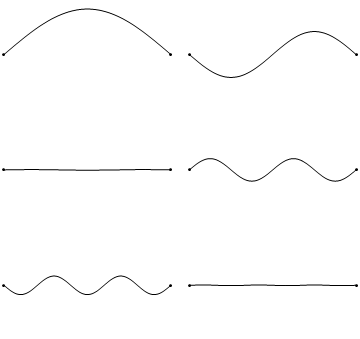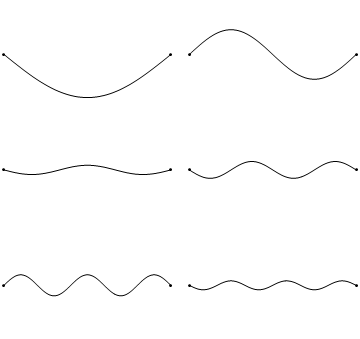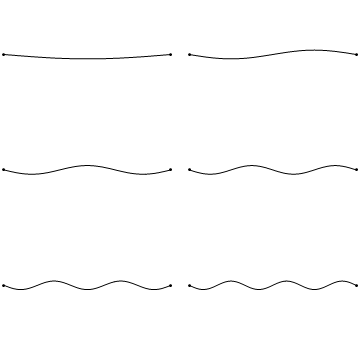
This is the most intuitive mode of vibration. When someone pulls a string back and lets it go, we would expect it to oscillate forwards and backwards, slowly losing energy until finally it comes to rest. This simple vibration DOES happen when a guitar is plucked, a piano string is struck, or a viola is bowed.

However, this is not the only possible way our string could vibrate. The animation on the top right shows the next simplest vibration that could occur. If you notice, this second animation has precisely half the wavelength as the first animation. This corresponds to a frequency twice as high pitched as the first animation. Sound familiar? This string corresponds to the first overtone of this string, with the top left animation corresponding to the fundamental. Each subsequent animation corresponds to the next overtone, ad nauseam. Now the amplitudes of each of these overtones is dependent on the string and instrument, but it is worth noting that ALL overtones and the fundamental are present. This is a major factor in the timbre of stringed instruments.

3.1.3. A Little Bit of Math

Think back to one period of a sine wave. The plot starts at the origin, rises to a maximum, crosses zero to reach a minimum, then comes back to zero in a position to repeat itself. Notice that the fundamental mode of vibration is exactly half of a sine wave - it starts at the first node, rises (or falls, depending on the time) to a max, and final returns to the second node. If we were to model this algorithmically, then we could use this equation:\[2L = λ\] where L is the length of our string and λ is the wavelength. Recall from the very first section that frequency is related to wavelength with this equation:\[f = \frac{v}{λ}\]

Where f is frequency and v is the wave velocity on the string. This is slightly different from the previous equation, where v was replaced with C (the speed of sound). Waves in strings follow a different rule when it comes to the speed they travel (as compared with simple media like air or water) - wave speed in strings is not dependent on the speed of sound in the material the string is made of.

To calculate v, we must consider two factors that will affect how quickly waves can travel through our string. One is tension (T, measured in Newtons). A taut string will allow waves to travel through it faster than a loose string, something that can be seen when plucking rubber bands stretched to different extremes. The other factor is linear mass density (μ, measured in kg/m). This is a measure of how much mass is present per length of string. A heavier string will slow down waves traveling through it. This can be observed in a guitar, where the thick bass E string vibrates visibly slower than the thin high E string. The relationship between tension, linear mass density, and velocity is shown in this equation: \[v = \sqrt{\frac{T}{μ}}\]

In short, velocity is proportional to the square root of tension and inversely proportional to the square root of linear mass density, which goes along with the example observations above. Combining these equations gives us the formula for the frequency of our fundamental frequency:\[f = \frac{1}{2L}\sqrt{\frac{T}{μ}}\] or, in general, for the nth overtone (or 0 for fundamental): \[f(n) = \frac{1+n}{2L}\sqrt{\frac{T}{μ}}\]

3.1.4. Acoustic Amplification

A string vibrating on its own does not move much air at all. It has such a thin profile that it is barely audible to anyone listening - think of an electric guitar with the power off. There are two techniques to amplify the sounds produced by a stringed instrument: couple the string to some kind of soundboard that will move much more air, or use an electronic amplifier.

In an acoustic guitar, lots of force is exerted on the bridge of the instrument, forcing it in close contact with the wood face of the guitar. When the strings are strummed, the bridge forces the wood face to vibrate at the same frequency as the strings. This moves much more air than the strings alone, which is then further amplified by the hollow chamber of the instrument. All of this amplification acts to add further complications to the overtones produced by the strings alone, giving the guitar its signature timbre. Similar processes occur in pianos and classical string instruments and every other acoustic stringed instrument - amplification is accomplished by a larger soundboard vibrating along with the strings, imparting onto the sound a new tone color.

Electric guitars use a magnet to pick up the vibrations of a steel string, and then convert that physical vibration into an electronic signal that can be amplified or distorted digitally. The same process that creates overtones in acoustic guitars applies to electric guitars, but that added timbre from the wood and chamber is lost in translation.