Timbre of Wind Instruments

Like stringed instruments, wind instruments produce standing waves that define their timbre. In strings, this standing wave production is easy to understand - the string is plucked, the wave travels until it hits an impedance (the nut or bridge), where a substantial portion of the wave is reflected. This closed string allows these vibrations to form quite complex standing wave systems due to the number of times the wave is reflected.

A similar process occurs in the air column in wind instruments, but the impedance in this case isn't a physical barrier. The sudden change to an open environment beyond the bell of the wind instrument reflects the vibrations back into the instrument proper, just like the string's attachment to the wood of a guitar. A change in impedance (even to less impedance) will reflect at least part of a wave. The open environment beyond the instrument provides less impedance than inside the instrument, so the vibrations of the air column are partially reflected. This produces a standing wave pattern that determines the timbre of the instrument.

3.2.1. Methods of Vibration

Wind instruments produce vibrations in one of three ways: they can use a reed, they can rely on the vibrating lips of the performer, and they can be shaped so that air interferes with itself to create vibrations. Most woodwinds work the first way, all brass work the second way, and flutes, recorders, and whistling lips work the third way.

When a clarinet player places the mouthpiece between their teeth and blows air, the small space between the mouthpiece and the reed will open and close rapidly. This causes air pressure inside the instrument to vary within the range of human hearing - the reed is responsible for the variations in air pressure discussed in the very first section.

From Wikimedia Commons

In brass instruments, the lips "buzz," and the rapid opening and closing of the lips creates the same rapid variations in pressure that occurs as a result of the mechanical reed in most woodwinds. This is why brass instruments are sometimes called lip reeds.

In a recorder, a small hole appears before any of the pitch holes. This splits the airstream, so that some of the air leaves the recorder at that point. As the air continues to reflect at the bell of the instrument, more an more of the air leaves through that exit hole. This creates interruptions in the air column that are periodic and in the range of human hearing, so the recorder can produce a sound! This interference is sometimes called an air reed.

3.2.2. Modes of Vibration

Strings must have nodes at their extremeties, because that is where they are attached to the nut and bridge of the instrument. Winds are different - they have a bell end that must be an antinode (because of the change in impedance), and another end that can either be a node or antinode depending on the instrument. Closed-pipe instruments have a node where the player's mouth is, while open-pipe instruments have an antinode. Let's examine how these constraints affect the modes of vibration in the air columns of these instruments.

Closed-pipe instruments

If we know that one end of a closed-pipe instrument is a node and the other is an antinode, then this is the simplest standing wave that can occur:

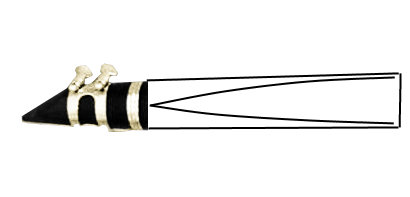
Notice that the wave that occurs is exactly a quarter of one sine wave period. We can show that through this relationship: \[λ = 4L\] where L is the length of the pipe. In strings we had to account for linear mass density and tension in finding the velocity of the wave. Luckily, in wind instruments the velocity of the wave is simply the speed of sound in air, about 343 m/s. Knowing this, we can write the equation for frequency like so: \[f = \frac{343 m/s}{4L}\]

Let's consider the next simplest standing wave. If we meet our conditions, it looks like this:

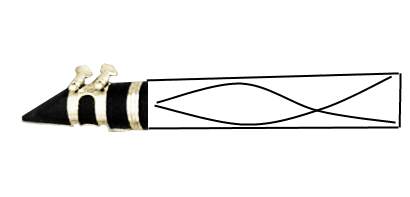
Notice this is exactly three quarters a single sine wave period. We can write this as \[λ = \frac{3 \times 343 m/s}{4L}\] Notice that this is exactly three times the equation we had earlier. Closed-pipe instruments only have odd overtones as a result of their nodal structure. We can find the nth harmonicof a closed-pipe instrument using the following equation: \[λ = \frac{n \times 343 m/s}{4L}\] where n is odd. Now there is an exception to this rule. If an instrument has a conical bore or flared end, then that instrument will have overtones like open-pipe instruments. For this reason, trombones and trumpets both have stronger even overtones while clarinets do not, despite all three of these instruments being closed-pipe.

Open-pipe instruments

If we know that both ends of an open-pipe instrument are antinodes, then this is the simplest standing wave that can occur:

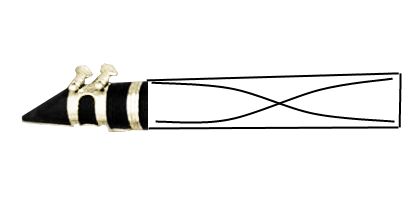
Notice that the wave that occurs is exactly a half of one sine wave period (shifted left by \(\frac{π}{4}\)). We can show that through this relationship: \[λ = 2L\] where L is the length of the pipe. Like before, the velocity of the wave is simply the speed of sound in air, about 343 m/s. Knowing this, we can write the equation for frequency like so: \[f = \frac{343 m/s}{2L}\]

Let's consider the next simplest standing wave. If we meet our conditions, it looks like this:

Notice this is exactly one period of a sine wave, again shifted left by \(\frac{π}{4}\), twice the frequency of the simplest mode of vibration. Unlike closed-pipe instruments, open-pipe instruments have even overtones. We can find the nth harmonic of an open-pipe instrument using the following equation: \[λ = \frac{n \times 343 m/s}{2L}\] where n is a natural number.

3.2.3. Changing Pitch

In strings, changing pitch is easy - the string can be effectively shortened and the pitch raised by a well-placed finger. In wind instruments, pitch isn't this straightforward. To start, pitch is affected by the radius of the pipe, not just length. In closed pipes, the effective length of the pipe is this: \[L + 0.61R\] where R is the radius of the pipe. In open pipes, this end effect is adjusted like so: \[L + 1.22R\] In short, the wider the radius of the pipe, the farther the air column goes outside the instrument before it is reflected. Be certain to adjust for the end effect when calculating pitch of pipes, because the physical length of the pipe is only part of the story.

There are two techniques to changing pitch in a wind instrument - changing the physical length of the pipe (in brass instruments) and using holes to change the effective length of the pipe (in woodwinds). Let's examine both of these in detail. If you haven't noticed yet, the pitching of wind instruments is extremely complicated and still not entirely well-understood, particularly in woodwinds. Keep this in mind as we study these instruments.

Brass

The song "Taps" is characterized by its interval jumps - no two notes are next to each other on a scale. This is because bugles are only able to play integer multiples of its fundamental frequency. If you have ever played a brass instrument, you know that certain lip buzzes "lock in" to the instrument and create beautiful tones, while others have a more vuvuzela toilet sound. This is because only standing waves that line up just right with the instrument's structure will produce a good sound. These partials, or good notes, are determined by instrument length, the bell and mouthpiece of the instrument, and the shape of the player's oral cavity and lips. But how do brass instrumentalists play notes that aren't on these partials?

The first attempt to solve this problem in brass instruments came with the nautral horn. This predecessor of the French horn had none of the valves we are familiar with today. These horns were designed so that their fundamental frequency was very low, but the range players could use was relatively high. Since the fundamental frequency determined how far apart the partials would be, they ended up being nearly scalar at common horn pitches. This allowed horn players to fake their way through scales. A good, in-tune chromatic scale still evaded instrumentalists however.

From Wikimedia Commons

The trombone was the first instrument that truly solved the pitch-change problem in brass instruments. Trombones have a slide that allows the length of the instrument to be lengthened and shortened at will. So long as the performer makes the proper oral adjustments, the instrument can slide between notes smoothly.

From Wikimedia Commons

The strategy tubas, trumpets, modern horns, and most other brass instruments take is using valves. When no valves are pressed, air flows straight through the instrument. However, when a valve is pressed, air is directed into a new pipe that lengthens the instrument, lowering its pitch. Using a combination of three different valves, trumpet players essentially control \(3! = 6\) different instruments, which they can switch between at will.

Woodwinds

Some of the first instruments created by humans were flutes made from animal bones. To this day, many children first learn to play music on a recorder, the essentially unchanged descendant of those ancient flutes. Woodwinds change pitch based on holes in the pipes. Contrary to popular belief, all the air from the instrument doesn't just rush out of the first open hole it encounters. Tiny holes have no effect at all on the instrument's pitch, and even larger holes will only shorten the instrument's effective length a little bit. The only time a hole will make the instrument effectively end at that point is if the hole takes up the diameter of the instrument. This is very impractical, considering enormous holes and structural integrity don't go together well.

So woodwinds use smaller holes in combination to change the effective length of the instrument. So where is the math for this relationship between hole size and instrument length?

Sadly, no equations like that exist. The relationship is simply too complex. Even closed holes add to the instrument's volume and change its pitch slightly, and holes beyond the first open one will still affect pitch. In short, woodwinds are built on trial-and-error, not hard-and-fast mathematics.

Even these incredibly complicated woodwinds have nothing on our final instrument family - the idiophones, explored in the next section.