Timbre of Idiophones

Idiophones, or instruments with bars or pipes (like xylophones and marimbas), have very complicated vibration patterns. We will be discussing these instruments, as well as membranophones (drums), in brief, because the mathematics involved are beyond the scope of these notes. If you are curious, I recommend Fletcher and Rossing's Physics of Musical Instruments for future reading.

3.3.1. Idiophones

Idiophones are fundamentally different than the other instruments we have studied thus far, because they do not naturally vibrate so that they have harmonic overtones - idiophones have overtones with ratios 1.0 : 2.76 : 5.40 : 8.90, not 1 : 2 : 3 : 4 as we've seen in all previous cases (except when only odd overtones appeared in closed-pipe instruments with cylindrical bores).

When struck, idiophones vibrate in one of two primary ways - they vibrate longitudinally, with particles in the wood or metal smashing into each other like the way sound travels through air; and they vibrate transversely, with the bar or pipe itself oscillating up and down in a standing wave, much like the way the strings we discussed earlier vibrate. The longitudinal vibration is very high in frequency relative to the transverse vibration, so we will only discuss transverse vibrations in this article. The nth mode of vibration, ignoring the longitudinal vibration, is given by the following equation: \[f_{n} = \frac{πvK(2n+1)^{2}}{8L^{2}}\] where v is the speed of sound in the material that comprises the idiophone; K is the radius of gyration \[K = \frac{\text{thickness of bar}}{3.46}\] for a flat bar, or \[K = \frac{\sqrt{\text{inner radius}^{2} + \text{outer radius}^{2}}}{2}\] for a tube; and L is the length of the bar or tube

As I said earlier, this relatively complicated formula for overtone pitches results in inharmonic overtones. This is a big problem, because when overtones are inharmonic our brains have a hard time working out the fundamental frequency. For this reason, hitting a plain old bar of wood isn't going to produce a recognizable pitch. Luckily, idiophone designers have taken advantage of the way a bar/pipe vibrates to take us towards harmonic overtones. However, before we understand this clever correction, we first must examine how the idiophone vibrates.

Because both ends of the bar are free, they must be antinodes in the transverse standing wave in the instrument. Therefore, the simplest mode looks like this:

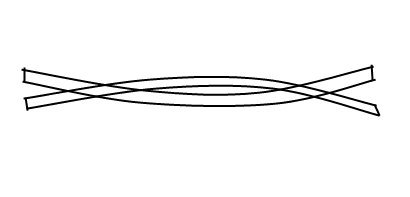
The second simplest mode that meets our conditions looks like this:

Notice that the center of the first mode of vibration is an antinode, while the second mode has a node at that point. If you were to remove some wood or metal at the center of the bar or pipe, then that area will be less stiff. This lowers the frequency of the first mode, but leaves the second mode unaffected (because that part of the bar does not move in the second mode).

To create a marimba, the instrument builder cuts away enough wood so that the first mode is lowered to exactly a quarter the frequency of the second mode. Xylophones are made similarly, but they are cut so that the first mode is a third the frequency of the second mode. The two octave difference in the marimba creates a sound darker than the bright xylophone, which has an octave-plus-a-fifth difference between its first and second modes.

The glockenspiel does not have material carved out of it in the same manner as xylophones and marimbas. However, the higher modes of vibration dampen very quickly in the instrument, leaving what is essentially a naked fundamental. This allows the listener to percieve a pure-sounding pitch, despite the shape of the bar.

3.3.2. Membranophones

Membranophones, like bass drums, have the most complex harmonic structure of any mortal instrument. Unlike idiophones, which effectively vibrate in one dimension, membranophones vibrate in two dimensions. For this reason, two numbers are needed to describe the modes of vibration of the drum head, rather than the one number we've used up until this point. For example, the fundamental mode is notated as \(u_{01}\) and looks like this:

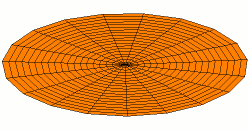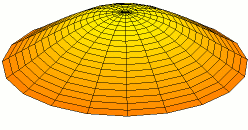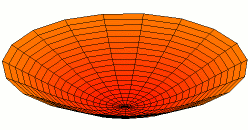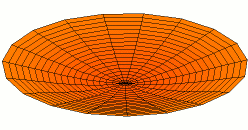
From Wikimedia Commons

All modes with the form \(u_{0x}\) will be comprised of concentric nodal lines and antinodal lines (while before our standing waves had points where nodes and antinodes occurred, in two dimensions entire lines behave as nodes and antinodes). For example, this is the \(u_{03}\) mode:

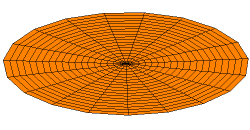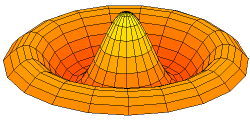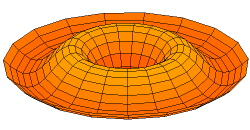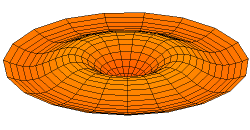
From Wikimedia Commons

As these numbers increase in size, the modes of vibration get extremely complicated - for example, this is mode \(u_{23}\):

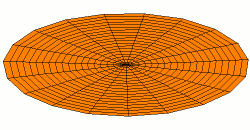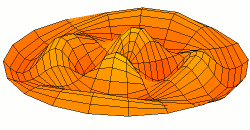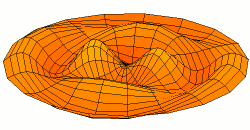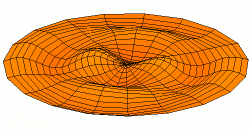
From Wikimedia Commons

I highly recommend using this applet to play around more with the different modes of vibration of drums.

The frequency of each mode of vibration in a circular drum head \(u_{mn}\) is given by \[f_{mn} = \frac{β_{mn}\sqrt{\frac{T}{σ}}}{2r}\] where \(r\) is the radius of the drum head, \(T\) is the tension of the drum head (measured in Newtons), \(σ\) is the area density (similar to linear mass density in strings), and \(β_{mn}\) is the \(n\text{th}\) zero value of this function: \[x^2\frac{d^2y}{dx^2}+x\frac{dy}{dx} + y(x^2 - m^2) = 0\] which some readers will recognize as the \(m\text{th}\)-order Bessel function.

These extremely complicated modes of vibration lead to crazy overtones, which cause most drums to convey no definite pitch. A bass drum, for example, has some harmonics in its lower modes, but the higher modes are louder and inharmonic and cause any pitch to be hidden.

But if these harmonics mask pitch, how then does a timpani work? Timpanis, for the unfamiliar reader, are drums that can change pitch via a pedal - the listener can clearly tell when a timpani is playing a Bb, for instance. The secret is the air locked into the timpani.

The air inside the timpani raises the frequency of modes that are circularly concentric, and lowers the frequencies of modes that are not. Because of this, the modes produce frequencies that roughly fall into the pattern 1 : 1.5 : 2 : 2.5. The modes that do not follow this pattern well (the ones that are circularly concentric) do not affect timbre much due to their rapid dampening. Because this pattern is well-ordered, our brains are able to percieve pitch from timpanis even as we cannot percieve definite pitch from a snare.